Как изменится дальность и точность, если вместо 363мм стволика прометус поставить >500мм прометеус (под глушитель) при условии 0,28 шаров и выхлопа в 140?
Я тут провел небольшое исследование. В результате чего получил вот такие графики. Взглянув на них можно сделать очень много выводов и дать ответ практически на любой поднимаемый здесь вопрос. За исключением: "Как изменится точность ?", но и при ответе на этот вопрос, нужно использовать эти результаты.
Условия моделирования:
1. Пружина имеет жесткость 1352 Н/м.
2. Масса шара 0.2 гр.
3. Масса поршня 14 гр. (вместе с головой поршня)
4. Давление воздуха 10^5 Па.
5. Рабочий ход поршня 5 см.
6. Диаметр цилиндра 24 мм.
7. Диаметр ствола 6.01 мм.
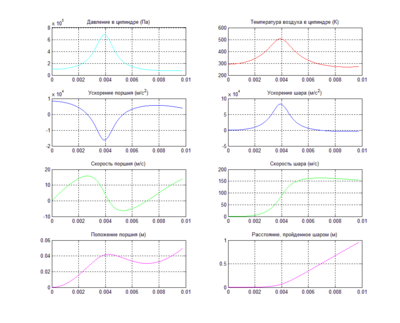
- Результаты моделирования.
Каждый из данных графиков показывает изменение некоторой физической величины во времени. Время изменяется от нуля до некоторого значения - это значение и говорит о том когда поршень ударится о голову цилиндра. Все физические величины измеряются в единицах в соответствии с системой СИ.
Нумерация графиков:
1 2
3 4
5 6
7 8
График 1 - Давление показывает как меняется давление воздуха в цилиндре и стволе (считается, что утечек воздуха нет). 10^5 Па - это как раз нормальное давление воздуха при температуре 293К (20С).
График 2 - Температура воздуха в цилиндре и стволе в градусах Кельвина (для получения температуры в градусах Цельсия нужно вычесть 273).
График 3 - Показывает изменение ускорения поршня во времени.
График 5 - Показывает как меняется скорость поршня со временем.
График 7 - Показывает положение поршня, считая от взведенного состояния (0 - взведен, 0.05 м. (5 см.) - спущен).
График 4 - Показывает как меняется ускорение шара.
График 6 - Показывает как меняется скорость шара.
График 8 - Показывает положение шара (т.е. то расстояние которое он уже успел пролететь по стволу).
Ну а теперь немного комментариев:
1. Поршень движется не поступательно (все время вперед, до тех пор пока не ударится о голову цилиндра) !

, а совершает колебательное движение ( в некоторый момент даже отскакивая назад ).
2. Шар перестает набирать скорость когда его ускорение становится равным 0 (примерно в момент времени равный 0.007 с .). За это время он проходит по стволу примерно 0.5 м. (т.е. делать ствол длиннее 0.5 м., при указанных исходных данных нет никакого смысла!

)
3. Скорость поршня в последний момент времени и определяет его энергию при ударе в голову цилиндра, и значит и нагрузку на гирбокс. Это к вопросу о том, выдержит ли гирбокс указанную пружину ? Предлагаю для ответа на данный вопрос следующее правило:
если энергия поршня в момент удара > чем в 2.5 раза превосходит таковую в базовом варианте, то ответ:
нет не выдержит (это если инженеры проектировали гирбокс с 2.5 кратным запасом прочности).
4. Отношение (Энергия шара / (Энергия шара + Энергия поршня)) * 100% и показывает КПД гирбокса. У меня это 65% для данных условий моделирования. Считаем что газ отдал всю энергию шару - это дупущение.
5. Вопрос для дальнейших раздумий: Как сделать так, чтобы поршень в последний момент времени имел нулевую скорость ? - в этом случае не будет удара в переднюю часть гирбокса.
6. Теорию про точность изложу здесь же чуть позднее.

